Experiments with magnets and our surroundings

Magnet math

In order to create and control magnetic fields in an exact way, we need to carefully understand how the strength of magnetic fields change depending on how far away you are from the magnet, what shape the magnet is, or if it is a solenoid or electromagnet.  We also need to understand how various materials react to magnetic fields.  In addition, we need to know what to call different parameters of magnets and fields and strengths and densities and so forth so we can intelligently communicate with one another.

Terms and definitions

First, let's use the right terms.  This is not as straightforward as it should be, since there are three different systems of units, and each system has different names for the same parameter!
Instead of recreating an excellent article, please hyperlink to it here for a set of terms and their definitions:  http://www.ee.surrey.ac.uk/Workshop/advice/coils/terms.html

Conversions

Since scientists may use the MKS system of units, or the CGS system of units, or the English system of units, sometimes you need to convert units from one system to another.  Every student learns some of this in high school, and every engineering and physics student becomes an expert at this in college.  Here is some conversion information where the units are equivalent.  For example, 1 Weber = 10^8 Maxwell.   The units marked with **** are those most textbooks today use.  You will notice that I often use lines of force and gauss and inches and amperes within this web site.

Equations and calculations

Now, for some equations regarding the variation of the strength of a magnetic field as the distance between you and magnet varies.  Here's a very nice site which has this information:  http://www.netdenizen.com/emagnet/  See also https://www.kjmagnetics.com/calculator.asp.

For additional information, jump to Magnetic Circuits.

Lenz's Law

Lenz's law is a basic law in electromagnetic theory for determining the direction of flow of induced currents. It was first stated by the Estonian physicist Heinrich Lenz (1804-65).

According to Lenz's law, when a current is caused to flow in an electrical conductor by a change in the external magnetic field surrounding the conductor, the direction of flow of the current is such as to produce a magnetic field opposing the original change in the external magnetic field.

This explains the behavior of magnets and conductors when one is moving relative to the other.  For example, when a conductor is moving across a magnetic field, a current is caused to circulate in the conductor producing a magnetic field which tries to stop the conductor from moving.  This is the basis for the experiments described in Pendulum, Copper Pipes and Magnetic Plumb.

Faraday's Law of Induction

Michael Faraday lived from 1791 to 1867.  In 1821, at the age of 30, he published an article titled, "On Some New Electromagnetic Motions" in the Quarterly Journal of Science.  This changed his life and our lives in a momentous way.

He was experimenting with magnets and wires, and noticed that as a wire was moved through a magnetic field, a voltage was induced or created within the wire.   If the wire was a part of a closed circuit, then current would flow.

Faraday stated that:
    Whenever a magnetic force increases or decreases, it produces electricity;
    the faster it increases or decreases, the more electricity it produces.

The voltage induced in the wire or conductor is proportional to the rate of change of the magnetic flux (how quickly the magnetic field is changing).  In other words, the faster the magnetic field is changing, the larger the voltage that is induced will be; or, the faster the wire is moving through the magnetic field, the larger the induced voltage will be.

This is the basis for how electric motors and electric generators work!

Lenz's law deals with the polarity of the induced voltage and the direction of the flow of current.

To learn more about Michael Faraday, check out this super book:
    Five Equations that Changed the World
    by Michael Guillen
    ISBN 0-7868-6103-7
    Hyperion
    NY  1995

Maxwell's equations

For hundreds of years, people only described with words the effect a magnet would have on other objects in general ways.  Then, during the 1800's, scientists started to describe these events more precisely, using numbers and formulas.  It changed from a qualitative description to a quantitative description.  In 1750, Franklin announced that lightning was electricity, electrical particles in motion.  In 1799, Volta created the first battery.  In 1819, Oersted discovered how an electric current affected a compass nearby.  In 1820, Ampere ...  In 1827, Ohm formulated his Ohms Laws which we all use today.  In xxxx, Gauss discovered how a negative electric charge can be isolated, but a north pole can not be isolated without a south pole.  In 1831, Faraday discovered how a changing magnetic field created an induced voltage, but did not describe it with a formula.  Then, in 1860,  Maxwell (1831-1879) put all of these together into a set of 4 equations which fully describes the relationships between current, electric fields and magnetic fields.   These are the 4 fundamental equations of electromagnetism.  They are the basis for how all electromagnetic devices function, and they explain a diverse range of phenomena which were previously unexplainable.

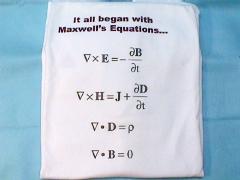  A great video:  https://www.youtube.com/watch?v=AWI70HXrbG0

This is a tee shirt from Ansoft Corporation, giving a summary of Maxwell's Equations.  What does it really mean? 

The first equation is really Faraday's Law of Induction.  It states that an induced electric field (E) is created by a changing magnetic flux density (dB/dt) with a polarity that opposes the changing magnetic field (-).  The faster the flux density changes, the greater the induced electric field.

In the second equation, Oersted and Ampere and Gauss showed that a current (J) would create a magnetic field (H).  However, Maxwell took it further and showed that a magnetic field (H) is created by a current (J) and a changing electric field (dD/dt).

In the third equation, Coulomb and Gauss showed that an enclosed electrical charge (p) will create a net electric field (D).  In other words, if you were to enclose an electron within a soap bubble, there would be a net electric field created by that electron which is a single negatively charged particle.

The fourth equation, also by Gauss, states that an enclosed magnet will have a net magnetic flux (B) of zero.  In other words, every magnet has a north pole and a south pole, so that if you were to enclose even a part of a magnet within a soap bubble, the total number of magnetic field lines entering the bubble would equal the total number of magnetic field lines exiting the bubble, with a net of zero.   Thus there is no monopole, or particle, which has just one magnetic pole without the other.  This would be like having a magnet with just a north pole, but no south pole.  Have you ever seen one?  No one has.  We don't think anyone ever will.

Good reference material:  http://www.phys.virginia.edu/classes/109N/more_stuff/Maxwell_Eq.html
                                                http://www-istp.gsfc.nasa.gov/Education/whmfield.html