

Experiments with magnets and our surroundings
Twelve Fundamentals of Magnetism
8. Permeability, µ [webers per ampere-turn-meter, Wb/(At*m)]
a. Links for this topic
http://en.wikipedia.org/wiki/Permeability_(electromagnetism)
b. What is it?
The permeability of a material is a measure of its ability to support a magnetic field within itself. It can be thought of as the effective multiplication of an external magnetic field by the alignment of the magnetic domains within the material.
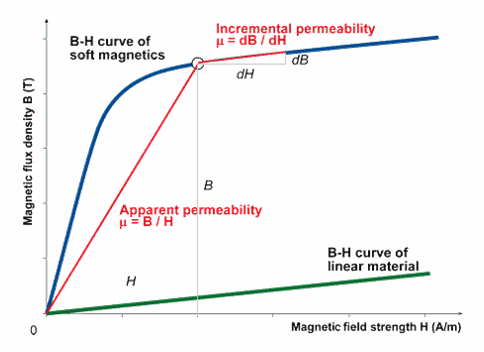
c. Its unit
Permeability, µ = B/H, the ratio of the flux density to the magnetic field intensity. It is often seen as B = µ*H. (µ is the lower case Greek letter mu.) Its units are webers per ampere-turn-meter (Wb/(At*m)) or newtons per ampere squared (N/A2). It can be seen as the slope of the B-H curve for a type of material. As H varies, the slope of B usually varies non-linearly. This is what causes some difficulty in designing magnetic circuits since B does not vary linearly with H for strongly magnetic materials. However, for most non-magnetic materials, its permeability is linear. See the diagrams below:
Here, we see how µ varies for different types of materials.
µf is the permeability of ferromagnetic material (strongly magnetic, but saturates, is non-linear)
(note, µf should look more like what we see below)
µp is the permeability of paramagnetic material (slightly magnetic, is linear)
µ0 is the permeability of a vacuum (non-magnetic, is linear)
µd is the permeability of diamagnetic material (slightly anti-magnetic, is linear)
Here, we see how both µf and B vary with respect to H for a ferromagnetic material, such as iron.
Since B = µ*H, when µ is non-linear, B will also be non-linear.
d. How is it used?
The permeability of a material is the product of the material's relative permeability with the permeability of a vacuum: µ = µr * µ0
i. µr is the relative permeability of the material, which usually ranges from 1 (for a vacuum) to 4,000 for an electrical steel
ii. In some special cases, the relative permeability can range from
0 for a superconductive material, to
0.9998 for a diamagnetic material, to
1,000,000 for special ferromagnetic alloys
ii. µr ~ 1 for most materials, such as a vacuum, air, wood, plastic, skin, copper, aluminum, silver, gold, etc
iii. µr has no units since it is a relative term
iv. µ0 (mu naught) = 4*pi*10-7 and is approximately equal to 1/800,000 Wb/(At*m)
e. An example in a vacuum
In a vacuum where µr = 1, so µ = µr * µ0 = 4*pi*10-7 , a field intensity of 796 At/m (often rounded to 800 At/m) is needed to create a flux density of 1mT within the vacuum. Since the permeability of a vacuum does not change, B is a linear function with respect to H. If you double H, B will double. So it would take about 800,000 At/m to create a flux density of 1 T within the vacuum.